주인장은 고등학생 수학 과외만 5년째 하고 있는 대학생이다..
2021수능(가형)이 현역이었고
2022, 2023, 2024는 수능을 응시하고 시험장에 가서 시험을 쳤었다.
운이 좋게도 국어(화작), 수학(미적분)은 2024까지 한 번도 1등급을 벗어난 적이 없었다. (물론 성적은 현역때가 제일 좋았다.)
2025수능은 일정이 안 돼서 못 봤고 혼자 수학만 풀어봤다.
이번 2026수능도 학교 수업을 빼기 힘들어서 못보고 수학만 좀 풀어보게 되었다.
과외를 오래 해서 그런지 아직 머리는 잘 돌아간다. 근데 현역 수능을 본지 5년이 지나.. 이제는 계산속도가 너무 떨어진다.
옛날 같으면 복잡한 식 적분이나 계산들 빠르게 슉슉 넘어갔을텐데, 요즘은 느릿느릿 계산해놓고도 이거 맞나 싶어서 한 번 더 쳐다보고 간다.
그래서 1시간 40분 안에 미적분까지 모든 문제를 다 풀수가 없다. (틀리는거랑 별개로..) 한 20분만 더 있으면 다 풀 것 같은데.
시험장 가서 집중모드로 풀었으면 좀 달랐으려나?
내가 각 문제들을 평가할 실력은 못 되고, 간단하게 풀이법이나 적을 얘기만 남기고 간다.
미적분, 확통까지 합쳐서 대충 2시간 반정도 푼 것 같고, 2문제 틀렸다.
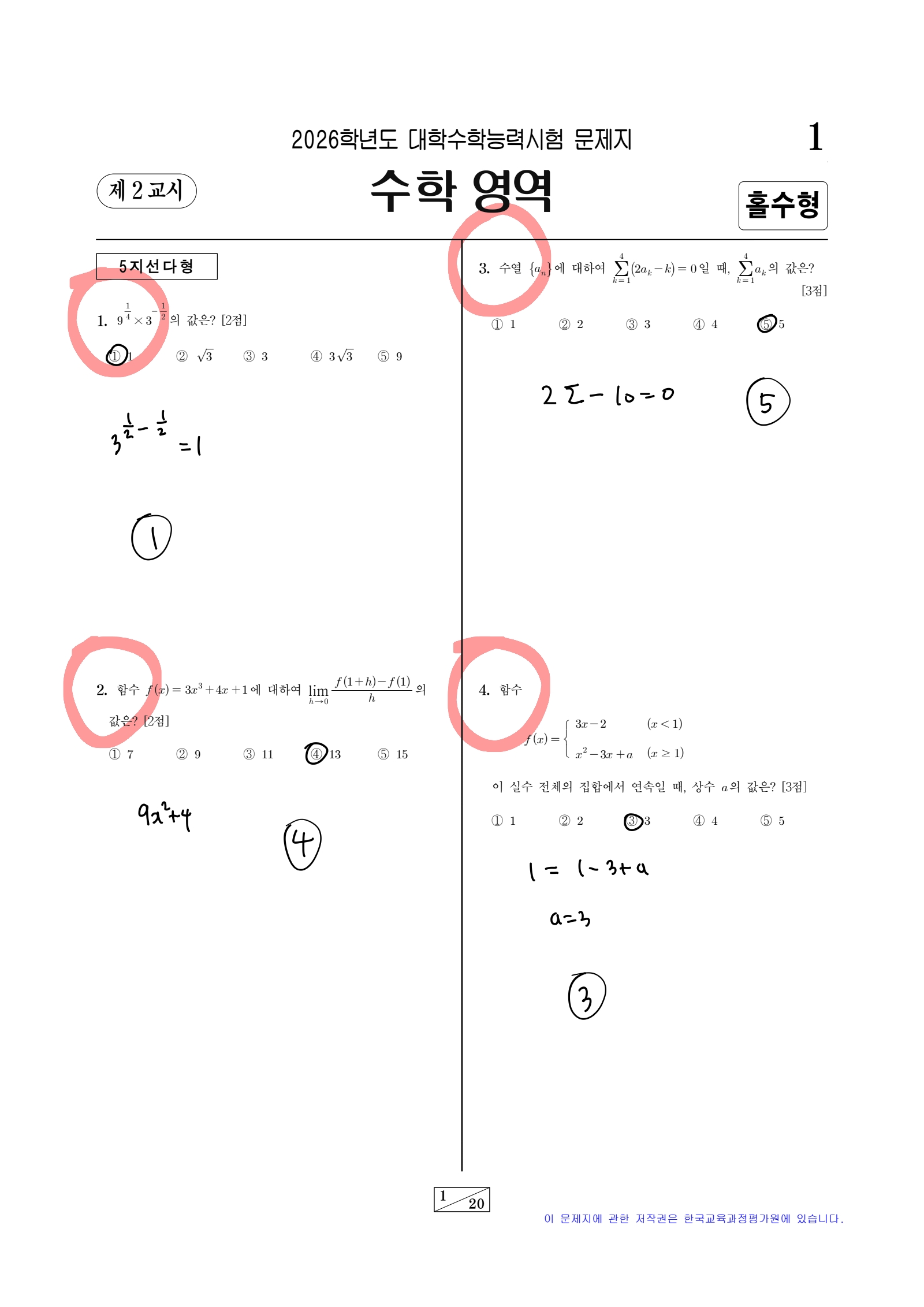
생략

생략

10번이 생각보다 쉽게 풀려 약간 당황했다. 쓸데없이 B점을 (t, 0)으로 놨는데, 그냥 (4, 0) 하면 되는거였는데...
이게 끝인가? 싶어서 한번 더 쳐다보고 넘어갔다.

11번 생략
12번은 9번보다 쉬우면서 왜 저 자리에 있을까?

13번 : 별로 어렵진 않은 문제인데, y축으로 둘러싸인 넓이 구해야 하는데 x축으로 둘러싸인 넓이 구해놓고 왜 답이 없냐면서 한참 고민했다... ㅋㅋㅋㅋㅋㅋㅋㅋㅋ
14번 : 드디어 어려운 문제. 삼각형 ABC가 5:4:3 직각삼각형이라 sin(BAC)를 알 수 있다. 이걸 이용해서 sin(CEG)를 구하기까지 식을 이어나가면 된다. 도형을 만지작거리다보면 중간에 턱 막힐텐데, AG에 선을 긋고 삼각형 ACG를 살펴보게 되면 푸는 길이 보인다.

15번 : h(x)가 하나의 극값이므로, h(x)를 미분한 g(x)-f(x)가 한 점에서만 서로 뚫고 지나가면 된다. 양수 부분에서 x가 아주 커지면 무조건 이차함수가 직선을 뚫고 올라가니까, 음수 부분에서 직선이 이차함수를 뚫지 않도록 하는 가장 큰 기울기(a값)을 찾으면 된다. 접할 때가 답!

옛날 같으면 19번같은 문제는 쉬운 4점으로 나왔을 거다. 2022수능 이후 수학이 선택과목화 되고 나서 전체적으로 시간이 빡빡해졌다. 2021수능까지는 확통이 있어서 시간이 많이 남았는데, 지금은 확통이 없어서 그런 것 같기도 하다.
20번 : (가)만 위에서 주어진 식 잘 갖다 넣어서 구하면 나머지는 쉽다.

21번 : 2024 수능 22번이 떠오르는 경우 잘 찍는 문제.... 잘못 찍고 맞는 경우라고 잘못 생각해서 틀렸다. 일단 g(x)가 연속이라 했으니 f(x)=0인 지점에서 t를 잡아야 하고, 모든 실수에 대하여 g(x) / x(x-2) 우극한이 존재해야 하니 g(0)=g(2)=0 이어야 한다. 그 다음에는 f(x)를 어디서 접냐와 0과 2가 어디냐를 잘 찍으면 된다. 하나 생각해야 할 것은, g(x) / x(x-2)의 우극한이 x=0과 x=2에서 우미분계수기는 한데 부호가 좀 달라진다는 점....
22번 : 점 A를 y=x에 대해 대칭이동한 점이 직선 OB위에 있다고 했는데.. 그래서 a와 b에 관한 식을 세웠을 것이다. 문자를 많이 만들기 싫은 사람은 점 B를 상수 k를 도입해서 (bk, ak)로 놓았을 텐데, 여기서 눈썰미가 좋았어야 한다. 풀이상 네모쳐놓은 1번식과 2번식에서 k=2이면 식이 성립한다는 걸 바로 찾았다면 5분컷. 못찾으면 30분동안 그것만 찾고있는거다. ㅋㅋㅋㅋㅋㅋㅋ 평가원도 원래 이렇게 지수로그함수 숫자 때려맞히는 문제를 냈었나? 하여튼, 문자 개수는 3개인데 식은 4개 주어지니 금방 풀리겠지 싶은데 숫자 못 맞히면 금방 안 풀린다. 주어진 로그함수의 역함수와 주어진 지수함수가 식이 좀 비슷해보이는걸 의심스럽게 봤어도 잘 풀었을 것이다.


생략

25번 같은 경우는 P(A 합 B) = P(A) + P(A^c 교 B) 성질을 사용하면 정말 쉽게 풀린다. 확통 과외 할 때 이거 꼭 좀 알고있으라고 항상 말하는데 제대로 쓰는 학생을 본 적이 없다. 앞으로 좀 더 자세히 알려줘야 할 듯..
26번 : 생략

27번 : 생략
28번 : 확통 객관식 마지막인 조건부확률 문제인데 생각보다 어려워서 놀랐다. 분모 구하는건 쉬운데.. 분자 구하는게 생각보다 머리를 좀 써야한다. (모든 공의 개수의 합이 홀수) and (상자3에 들어있는 공이 상자2에 들어있는 공보다 1개 많음) 경우의 수를 구해야 하니까. 아마 분모를 구할때 홀홀홀짝 / 홀짝짝짝으로 구했을 거라 이 분류를 따라갔을 텐데, 은근 머리아프다.

29번 : 이항분포의 정규분포화 문제. 생략
30번 : 중복조합인지 뭔지,,, 그냥 경우의수 문제. 공이 1개인 주머니랑 2개인 주머니 개수로 가능한 경우를 찾아 분류했을텐데, 주머니가 2 2 1 1 1 1 0 0 0 0 로 되는 경우를 구하는게 어렵다. 2가 맨 끝에 있으면 옆에 0이 하나만 붙어있어도 되고, 2 0 2 0 조합으로 있으면 또 0이 하나씩만 붙어있어도 되고, 등등.... 머리 잘 써서 가능한 경우를 다 찾으면 답이다. 난이도는 28번이랑 비슷하다고 생각된다.
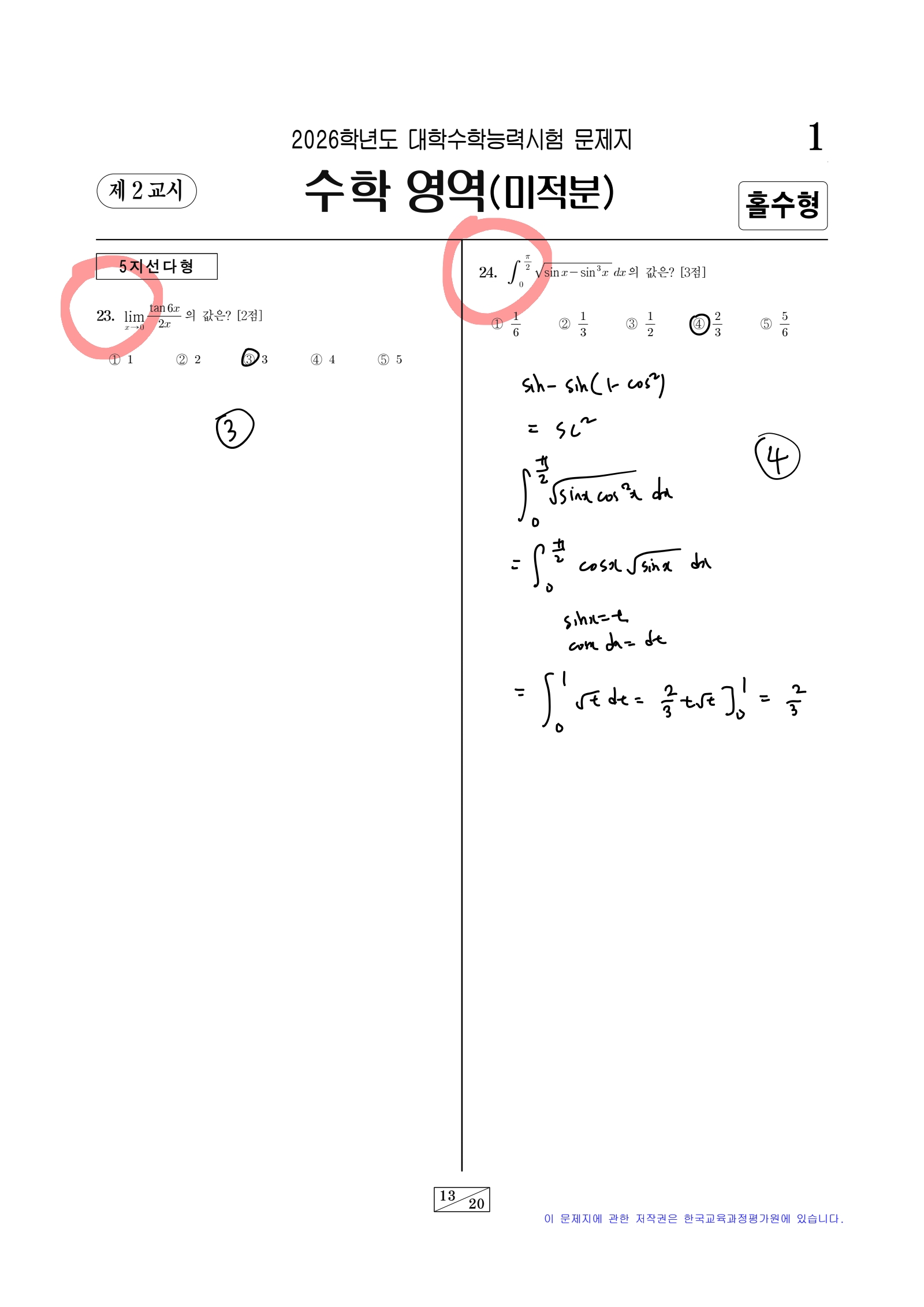
24번 : 오랜만에 보는 치환적분! 최근 미적분을 가르칠 일이 없다보니 아주 반가운 문제였다..

26번 : 정삼각형의 넓이 (루트3/4) * (한변길이)^2 이거 기억해두면 쓸일 많다. 몰라도 지장없지만.

27번 : 어우,, 당황하지 않고 침착하게 미분.
28번 : 어렵게 생겼는데 그냥 역함수 적분하는 문제. 인테그랄 g(t)dt에서 그냥 t를 s로 치환해버리면 해결. 위아래끝도 구하기 어렵지 않게 줬다. 근데 적분 계산이 정말 귀찮게 나와서 계산하는데 애를 좀 먹었다. 이런게 현역 때랑 지금 풀 때랑 차이점이다. 현역이었으면 순식간에 계산 다 했을 듯.

29번 : 다풀어놓고 a_2에다가 16 써서 당당하게 틀림; a_2는 1/2이다. b_1을 찾는 과정에서만 헤매지 않는다면 금방 풀 문제. 요즘은 수열 문제에서 범위 주고 만족하는 경우 찾는 기출이 많아서 열심히 공부했다면 쉽게 풀었을 듯?
30번 : 이 문제도 참,,, 열심히 풀면 풀린다. 특별히 어려운 것도 없고... 그냥 계산이 복잡할 뿐... 그림 열심히 그리면 된다... b값이 직접 구해지지 않아서 마지막에 (lnb/b)를 구하는게 약간 헷갈리는데 2020 수능 수학 가형 30번이랑 식이 비슷하게 생겨서 그 문제를 풀었던 학생이면 "아 b값을 직접 구하라는게 아니구나" 깨닫고 해결할 수 있었을 것이다.
전체적으로 가장 어려운 문제 : 21, 22번
공통 어려운 문제 : 21 > 22 > 14
확통 어려운 문제 : 28 = 30
미적분 어려운 문제 : 30 > 28
최근 수능들을 보면 다 공통문제가 어려운 것 같다.
이정도 미적분이면 LATTE(2018~2021 시절) 기출에 비해서는 많이 쉬워진 편이라는 생각이다.
그런데도 확통이랑 미적분 등급컷이 한문제씩 차이나는건 아직까지도 확통이 미적분보다 쉽기 때문인 듯.
만점을 맞으려면 확통도 공부 많이 해야하지만, 한문제정도만 틀리는게 목표라면 확통이 미적분보다 훨~~~~씬 쉽다.
그러므로 무조건 선택 만점을 맞아서 이득을 보고싶다는 생각이 아니라면 확통을 선택하는게 좋지 않을까?
'공부' 카테고리의 다른 글
| 교통기사 자격증 취득 후기 (1) | 2025.09.13 |
|---|